1.  Сферически симметричные решения

Прежде всего попробуем отыскать какую-нибудь функцию попроще, удовлетворяющую уравнению Гамильтона. Хотя волновая функция $\Psi (r,\theta,\varphi, t)$ в общем случае зависит от углов $\theta$ и $\varphi$ , можно поискать такой особый случай, когда она не зависит от углов. Оказывается, что атом водорода находится в таком состоянии, когда его орбитальный момент импульса равен нулю. Это состояние называют к $1s$ -состояниемк (можно считать, что $s$ от слова к сферически симметричныйк). В этом случае в полном лапласиане останется только первое слагаемое и после подстановки в полученное уравнение Шредингера волновой функции $\Psi ({\bf r}, t)$ и сокращения на экспоненциальный множитель оно сильно упростится:

$$\frac{1}{r}\frac{d^2}{dr^2}(r\psi)=-\frac{2}{\hbar^2}\left(E+\frac{e^2}{r}\right)\psi,$$ (1.4)

где функция Гамильтона этого состояния обозначена через $E$ .

Еще до создания квантовой механики экспериментальное изучение спектра водорода показало, что состояния системы описываются формулой

$$E_{n}=- E_{R}\frac{1}{n^2},$$ (1.5)

где $E_{R}$ - постоянная Ридберга, как это следует из измерений, равная примерно $13,6$эв . Затем Бор построил модель, которая привела к тому же уравнению и предсказала, что $E_{R}$ должно равняться $me^4/2\hbar^2$ .

Прежде чем заняться решением упрощенного уравнения Шредингера, изменим масштаб и уберем из него все лишние константы вроде $e^2,\hbar$ . От этого выкладки станут легче. Если сделать подстановки

$$r=\frac{\hbar^2}{e^2}\rho \qquad E=\frac{e^4}{2\hbar^2}\varepsilon,$$ (1.6)

то уравнение Шредингера обратится (после умножения на $\rho$ ) в

$$\frac{d^2(\rho\psi)}{d\rho^2}=-\left(\varepsilon+\frac{2}{\rho}\right)\rho\psi .$$ (1.7)

Раз произведение $\rho\psi$ встречается в обеих частях уравнения, то лучше работать с ним, чем с самим $\psi$ . Обозначив $\rho\psi=f$ , мы получим уравнение, которое выглядит проще:

$$\frac{d^2 f}{d\rho^2}=-\left(\varepsilon+\frac{2}{\rho}\right)f.$$ (1.8)

Теперь предстоит найти функцию $f$ , которая удовлетворяет полученному уравнению, т. е. просто решить дифференциальное уравнение. Хоть уравнение не из легких, но его можно решить при помощи следующей процедуры. Во-первых, заменим $f$ , которое является некоторой функцией от $\rho$ , произведением двух функций:

$$f(\rho)=e^{-\alpha\rho}g(\rho).$$ (1.9)

Это просто означает, что мы выносим из $f(\rho)$ множитель $e^{-\alpha\rho}$ . Для любого $f(\rho)$ это можно сделать. Задача теперь просто свелась к отысканию подходящей функции $g(\rho)$ .

Подставив значение $f(\rho)$ в уравнение для функции $f$ , получим уравнение для $g$ :

$$\frac{d^2g}{d\rho^2}-2\alpha\frac{dg}{d\rho}+\left(\frac{2}{\rho}+\varepsilon+\alpha^2\right)g=0.$$ (1.10)

Мы вправе выбрать любое $\alpha$ , поэтому сделаем так, чтобы было $\alpha^2=-\varepsilon$ , тогда получим

$$\frac{d^2g}{d\rho^2}-2\alpha\frac{dg}{d\rho}+\frac{2}{\rho}g=0 .$$ (1.11)

Этому уравнению можно удовлетворить некоторой функцией $g(\rho)$ , которая записывается в виде ряда

$$g(\rho)=\sum_{k=1}^{\infty}a_{k}\rho^k ,$$ (1.12)

где $a_{k}$ - постоянные коэффициенты. И нам осталось только найти подходящую бесконечную последовательность коэффициентов $a_{k}$ ! Проверим, годится ли такая запись решения. Первая производная такой функции $g(\rho)$ равна

$$\frac{dg}{d\rho}=\sum_{k=1}^{\infty}a_{k}k\rho^{k-1} ,$$ (1.13)

а вторая

$$\frac{d^2g}{d\rho^2}=\sum_{k=1}^{\infty}a_{k}k(k-1)\rho^{k-2} .$$ (1.14)

Подставляя это в уравнение для $g(\rho)$ , получим

$$\sum_{k=1}^{\infty}k(k-1)a_{k}\rho^{k-2}-\sum_{k=1}^{\infty}2\alpha ka_{k}\rho^{k-1}+\sum_{k=1}^{\infty}2a_{k}\rho^{k-1}=0.$$ (1.15)

Если первую сумму заменить некоторым ее эквивалентом, то все выражение станет выглядеть лучше. Первый член в сумме равен нулю, поэтому каждое $k$ можно заменить на $k+1$ , от этого ничего в бесконечном ряде не изменится. Значит, первую сумму мы вправе записать и так:

$$\sum_{k=1}^{\infty}(k+1)ka_{k+1}\rho^{k-1} .$$ (1.16)

Теперь можно объединить все три суммы в одну:

$$\sum_{k=1}^{\infty}[(k+1)ka_{k+1}-2\alpha ka_{k}+2a_{k}]\rho^{k-1}=0 .$$ (1.17)

Этот степенной ряд должен обращаться в нуль при всех мыслимых значениях $\rho$ , что возможно лишь тогда, когла коэффициенты при каждой степени $\rho$ порознь равны нулю. Мы получим решение для атома водорода, если отыщем такую последовательность $a_{k}$ , для которой

$$(k+1)ka_{k+1}-2(\alpha k-1)a_{k}=0$$ (1.18)

при всех $k>1$ . А это легко устроить. Выберем какое угодно $a_{1}$ . Зтем все прочие коэффициенты образуем с помощью формулы

$$a_{k+1}=\frac{2(\alpha k-1)}{k(k+1)}a_{k}.$$ (1.19)

Пользуясь ею, мы получим $a_{2}, a_{3}, a_{4}$ и т. д. , и каждая пара будет удовлетворять необходимой последовательности. Мы получим ряд для $g(\rho)$ , являющийся решением уравнения для $g$ . С его помощью мы напишем $\psi$ - решение уравнения Шредингера. Обратим внимание на то, что решения зависят от того, какова предполагаемая функция Гамильтона (через $\alpha$ ), но для каждого значения $\varepsilon$ получается свой ряд.

Решение-то у нас есть, но что оно представляет физически? Понятие об этом мы получим, посмотрев, что происходит вдалеке от протона - при больших $\rho$ . Там основное значение приобретают наивысшие степени членов ряда, т. е. надо посмотреть, что бывает при больших $k$ . Когда $k\gg 1$ , то предыдущее уравнение (1.19) приближенно совпадает с

$$a_{k+1}=\frac{2\alpha}{k}a_{k ,}$$ (1.20)

а это означает, что

$$a_{k+1}\approx \frac{(2\alpha)^k}{k!} .$$ (1.21)

Но это как раз коэффициенты разложения в ряд $e^{+2\alpha\rho}$ . Функция $g$ оказывается быстро растущей экспонентой. Даже после умножения на $e^{-\alpha\rho}$ получающаяся функция $f(\rho)$ (см. 1.9) будет при больших $\rho$ меняться как $e^{\alpha\rho}$ . Мы нашли математическое решение, но оно не является физическим. Оно представляет случай, когда электрону менее всего вероятно очутиться вблизи протона! Чаще всего он вам повстречается на очень больших расстояниях $\rho$ . А волновая функция для связанного электрона должна при больших $\rho$ стремиться к нулю.

Нужо подумать, а нельзя ли как - нибудь сделать решение физичным. Оказывается, можно. Посмотрите! Если бы, по счастью, оказалось, что $\alpha=1/n$ , где $n$ - любое целое число, то уравнение (1.19) привело бы к $a_{n+1}=0$ . И все высшие члены обратились бы тоже в нуль. Вышел бы не бесконечный ряд, а конечный многочлен. Любой многочлен растет медленнее, чем $e^{\alpha\rho}$ , поэтому множитель $e^{-\alpha\rho}$ наверняка забьет его при больших $\rho$ , и функция $f$ при больших $\rho$ , будет стремиться к нулю. Единственные решения для связанных состояний это те, для которых $\alpha=1/n$ , где $n=1, 2, 3, 4$ и т. д.

Оглядываясь на уравнение (1.11) и вспоминая, что $-\varepsilon=\alpha^2$ , мы видим, что у сферически симметричного волнового уравнения могут существовать решения для связанных состояний лишь при

$$-\varepsilon=1,\;\frac{1}{4}, \;\frac{1}{9}, \;\frac{1}{16},\cdots, \;\frac{1}{n^2}, \cdots .$$ (1.22)

Допустимы только те состояния, которые составляют именно такую часть величины $e^4/2\hbar^2$ , т. е. функция Гамильтона $n$ -го уровня равна

$$E_{n}=-\frac{e^4}{2\hbar^2}\frac{1}{n^2}.$$ (1.23)

Кстати, ничего мистического в отрицательных функциях Гамильтона нет. Они отрицательны просто потому, что когда мы решили писать $U=-e^2/r$ , то тем самым в качестве нуля выбрали состояние электрона, расположенного вдалеке от протона. Когда он ближе, то его функция Гамильтона ниже нуля, она ниже всего (самая отрицательная) при $n=1$ и возрастает к нулю с ростом $n$ . Первым большим успехом теории Шредингера явилось то, что она смогла воспроизвести этот результат прямо из основного уравнения движения электрона.

Теперь, когда мы рассчитали наш первый атом, рассмотрим свойства полученного решения. Объединим все выделившиеся по дороге факторы и выпишем окончательный вид решения:

$$\psi_{n}=\frac{f_{n}(\rho)}{\rho}=\frac{e^{-\rho/n}}{\rho}g_{n}(\rho),$$ (1.24)

где

$$g_{n}(\rho)=\sum_{k=1}^n a_{k}\rho^k$$ (1.25)

и

$$a_{k+1}=\frac{2(k/n-1)}{k(k+1)}a_{k}.$$ (1.26)

Пока нас интересует главным образом относительная вероятность обнаружить электрон в том или ином месте, можно в качестве $a_{1}$ выбирать любое число. Возьмем, например, $a_{1}=1$ . (Обычно выбирают $a_{1}$ так , чтобы волновая функция была "нормирована", т. е. чтобы полная вероятность обнаружить электрон где бы то ни было в атоме была равна единице. Мы в этом сейчас не нуждаемся.)

В низшем состоянии $n=1$ и

$$\psi_{1}(\rho)=e^{-\rho}.$$ (1.27)

Если атом водорода находится в своем основном (наиболее низком) состоянии, то амплитуда того, что электрон будет обнаружен в каком - то месте, экспоненциально падает с расстоянием от протона. Характерное расстояние, на котором он встречается, составляет около одного $\rho$ или $r=\frac{\hbar^2}{e^2}$ .

Подстановка $n=2$ дает следующий более высокий уровень. В воловую функцию этого состояния входят два слагаемых. Она равна

$$\psi_{2}=\left(1-\frac{\rho}{2.}\right)e^{-\rho/2}.$$ (1.28)

Волновая функция для следующего уровня равна

$$\psi_{3}=\left(1-\frac{2\rho}{3}+\frac{2}{27}\rho^{2}\right)e^{-\rho/3}.$$ (1.29)

Эти три волновые функции приведены на (Рис. 3.2). Общая тенденция уже видна. Все волновые функции при больших $\rho$ , поколебавшись несколько раз, приближаются к нулю. И действительно, число "изгибов" у $\psi_{n}$ как раз равно $n$ , или, если угодно, число пересечений оси абсцисс - число нулей - равно $n-1$ .

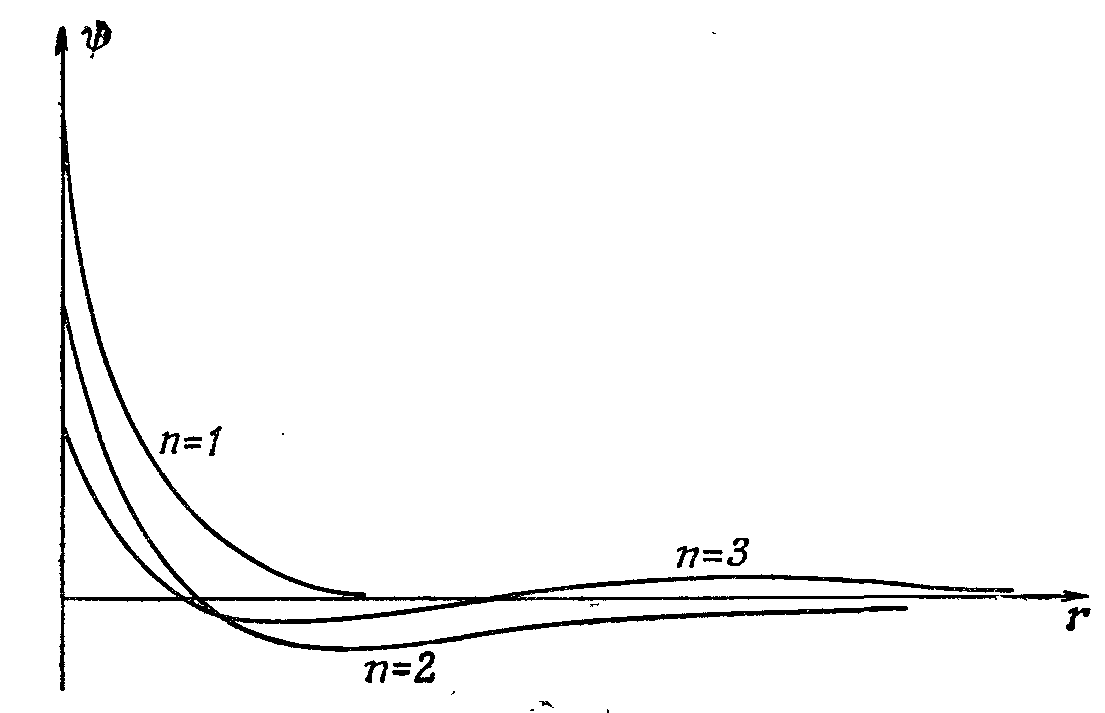Рис. 3.2.  Волновые функции трех первых состояий атома водорода с $l=0$ .

Масштабы выбраны так, чтобы полные вероятности совпадали