2.  Общее решение для водорода

Мы нашли, что в состояниях, описываемых волновой функцией $\psi_{n}(r)$ , амплитуда вероятности обнаружить электрон зависит только от $r$ - расстояния до протона. Момент импульса таких состояний равен нулю. Теперь займемся состояниями, у которых какой - то момент импульса имеется.

Представим себе некоторое возможное состояние электрона; внутренняя угловая структура этого состояния будет определяться квантовым числом $l$ . Электрон на оси $z$ не может иметь какого - либо орбитального момента относительно этой оси. Но пусть тогда $m=0$ . Вот это другое дело; теперь уже может появиться не равная нулю амплитуда того, что электрон окажется на оси $z$ на таком - то расстоянии от протона. Обозначим эту амплитуду $F_{l}(r)$ . Это - амплитуда того, что электрон будет обнаружен на расстоянии $r$ по оси $z$ , когда атом находится в состоянии $\vert l , 0\rangle$ , т. е. в состоянии с орбитальным моментом $l$ и его $z$ - компонентой $m=0$ .

А если нам известно $E_{l}(r)$ , то известно все. Теперь уже в любом состоянии $\vert l, m \rangle$ мы можем узнать амплитуду $\psi_{l,m}(r)$ того, что электрон обнаружится в произвольном месте атома. Например, пусть у нас есть атом в состоянии $\vert l, m \rangle$ . Какова амплитуда того, что электрон обнаружится под углом $\theta,\varphi$ и на расстоянии $r$ от начала? Проведите новую ось $z$ , скажем $z^{\prime}$ , под этим углом (Рис. 3.3) и задайте вопрос: какова амплитуда того, что электрон окажется на новой оси $z^{\prime}$ на расстоянии $r$ ? Когда $m^{\prime}=0$ , то амплитуда того электрон обнаружится на оси $z^{\prime}$ , есть $F_{l}(r)$ . Результат получится перемножением двух амплитуд. Первая это амплитуда того, что атом, находящийся в состоянии $\vert l, m \rangle$ относительно оси $z$ , окажется в состоянии $\vert l, m^{\prime}=0\rangle$ относительно оси $z^{\prime}$ . Умножим эту амплитуду на $F_{l}(r)$ и мы получим амплитуду $\psi_{l,m}({\bf r})$ того, что электрон обнаружится в точке $(r,\theta,\varphi)$ относительно первоначальной системы осей.

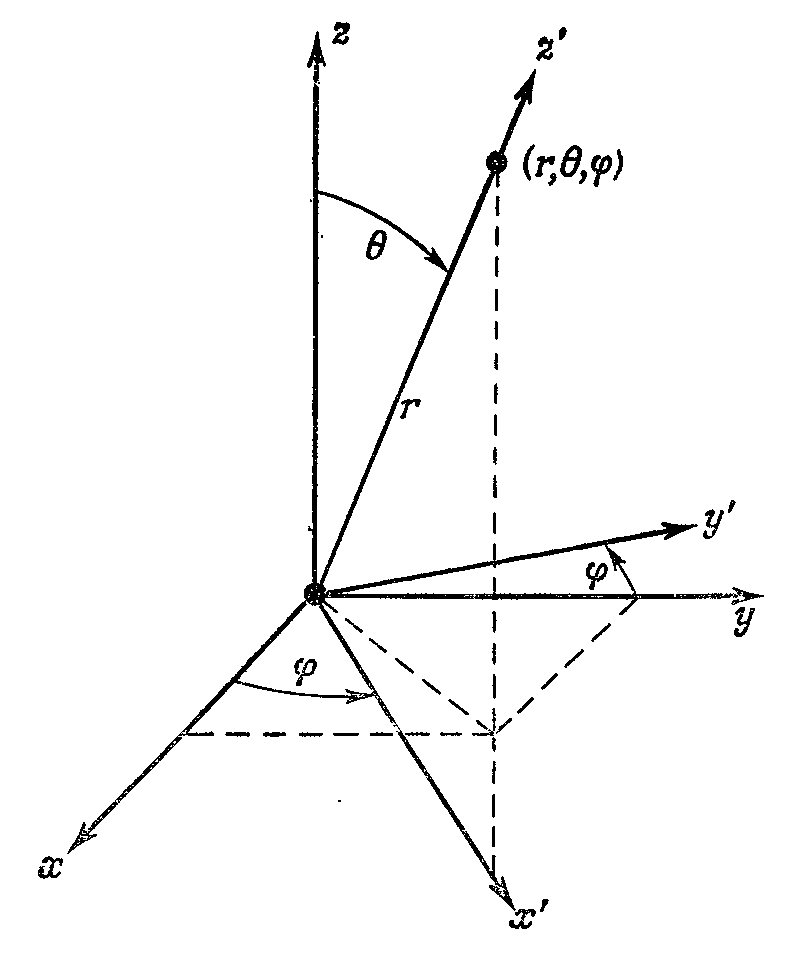Рис. 3.3. Точка $(x, y, z)$ лежит на оси $z'$ системы координат $x', y', z'$ .

Матрицы преобразования для поворотов нам известны. Чтобы перейти от системы $x,y,z$ к системе $x^{\prime},y^{\prime},z^{\prime}$ (Рис. 3.3), можно сперва сделать поворот вокруг оси $z$ на угол $\varphi$ , а потом сделать поворот вокруг новой оси $y$ (оси $y^{\prime}$ ) на угол $\theta$ . Совместный поворот выразится произведением

$$R_{y}(\theta)R_{z}(\varphi).$$ (2.30)

Амплитуда того, что после поворота обнаружится состояние $\vert l, m^{\prime}=0\rangle$ , есть

$$\langle l, 0 \vert R_{y}(\theta) R_{z}(\varphi) \vert l, m\rangle.$$ (2.31)

В итоге получаем

$$\psi_{l, m}({\bf r})=\langle l, 0 \vert R_{y}(\theta) R_{z}(\varphi) \vert l, m\rangle F_{l}(r) .$$ (2.32)

В этих обозначениях волновые функции атома водорода чаще всего записываются так:

$$\psi_{l, m}({\bf r})=Y_{l, m}(\theta, \varphi)F_{l}(r)$$ (2.33)

Эти волновые функции должны быть решениями дифференциального уравнения (0.2). Подставим значение $\psi_{l,m}({\bf r})$ в (0.2) и получим

$$\begin{multline} \frac{Y_{l, m}}{r}\frac{\partial^2}{\partial r^2}(rF_{l})+\frac... ...ac{2}{\hbar^2}\left(E+\frac{e^2}{r}\right)Y_{l, m}F_{l}. \nonumber\end{multline}$$

(2.34)

Помножим все на $r^2/F_{l}$ и перегруппируем слагаемые; результат будет таков:

$$\begin{multline} \frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\t... ...^2}\left(E+\frac{e^2}{r}\right)\right\}\right]Y_{l, m} . \nonumber\end{multline}$$

(2.35)

Левая часть этого уравнения зависит от $\theta$ и $\varphi$ , а от $r$ не зависит. Какое бы значение $r$ мы ни взяли, от этого левая часть не изменится. Значит, то же должно быть выполнено и для правой части. Хотя в выражении в квадратных скобках там и сям попадаются разные $r$ , все выражение от $r$ зависеть не может, иначе бы не получилось уравнение, которое годится для всех $r$ . Кроме того, как мы видим, эта скобка не зависит ни от $\theta$ , ни от $\varphi$ . Она должна быть постоянным числом. Его величина имеет право зато зависеть от значения $l$ того состояния, которое мы изучаем, поскольку этому состоянию принадлежит функция $F_{l}$ ; поэтому постоянное число мы обозначим $K_{l}$ . Предыдущее уравнение, стало быть, равнозначно двум уравнениям

$$\frac{1}{\sin\theta}\frac{\partial}{\partial\theta}\left(\sin\the... ...c{1}{\sin^2\theta}\frac{\partial^2Y_{l, m}}{\partial\varphi^2}=-K_{l}Y_{l, m} ,$$ (2.36)

$$\frac{1}{r}\frac{\partial^2}{\partial r^2}(rF_{l})+\frac{2}{\hbar^2}\left(E+\frac{e^2}{r}\right)F_{l}=K_{l}\frac{F_{l}}{r^2} .$$ (2.37)

Для каждого состояния, описываемого числами $l$ и $m$ , мы знаем функции $Y_{l, m}$ ; тогда из уравнения (2.36) можно определить $K_{l}$ . Затем,подставив $K_{l}$ в (2.37), мы получим дифференциальное уравнение для функции $F_{l}(r)$ . Если мы его сможем решить, то все множители, входящие в (2.33), нам станут известны, и мы узнаем $\psi({\bf r})$ . Во - первых, заметим, что при всех $m$ (входящих в данное $l$ ) число $K_{l}$ должно быть одним и тем же, поэтому мы вправе выбрать в $Y_{l, m}$ то $m$ , какое нам нравится, и вставить его в (2.36). Проще всего взять $Y_{l,l}$ . Тогда

$$R_{z}(\varphi) \vert l, l\rangle=e^{il\varphi} \vert l, l\rangle .$$ (2.38)

Матричный элемент $R_{y}(\theta)$ тоже совсем прост:

$$\langle l, 0 \vert R_{y}(\theta) \vert l, l\rangle=b(\sin\theta)^l ,$$ (2.39)

где $b$ - некоторое число. Объединяя их, получаем

$$Y_{l, l}\sim e^{il\varphi}\sin^{l}\theta .$$ (2.40)

Подстановка этой функции в (2.36) даст

$$K_{l}=l (l+1) .$$ (2.41)

Теперь, когда мы определили $K_{l}$ , уравнение (2.37) даст нам радиальную функцию $F_{l}(r)$ . Перед нами обычное уравнение Шредингера, у которого угловая часть заменена ее эквивалентом $K_{l}F_{l}/r^2$ . Перепишем (2.37) в той форме, в какой мы писали уравнение (1.4):

$$\frac{1}{r}\frac{d^2}{d r^2}(rF_{l})=-\frac{2}{\hbar^2}\left\{E+\frac{e^2}{r}-\frac{l(l+1)\hbar^2}{2r^2}\right\}F_{l}.$$ (2.42)

У потенциала положения появилась какая - то таинственная добавка. Хотя она появилась на свет после длинной серии математических шагов,тем не менее у нее простое физическое происхождение. Можно продемонстрировать ее появление при помощи полуклассических аргументов. После этого она уже не будет выглядеть таинственно.

Представим классическую частицу, вращающуюся вокруг некоторого центра взаимодействия. Функция Гамильтона этой системы сохраняется и является суммой потенциалов положения и кинетического

$$U=U(r)+\frac{1}{2}V^2=const.$$ (2.43)

В общем случае $V$ разлагается на радиальную компоненту $v$ и на касательную компоненту $r\dot\theta$ , т. е.

$$V^2=v^2+(r\dot\theta)^2.$$ (2.44)

Момент импульса $r^2\dot\theta$ тоже сохраняется; пусть он равняется $L$ . Тогда можно написать

$$r^2\dot\theta=L, \qquad \mbox {или} \qquad r\dot\theta=\frac{L}{r},$$ (2.45)

т. е. потенциал положения равен

$$U(r)=\frac{e^2}{r}+\frac{L^2}{2r^2}.$$ (2.46)

Если вернуться к обозначениям принятым в функции Гамильтона, то увидим, что:

$$\frac{L^2}{2r^2}=\frac{1}{2}\frac{C_{12}}{T^2_{12}}.$$ (2.47)

Но эта величина почти точно совпадает с добавкой (2.42). Единственная разница в том, что вместо ожидаемого числителя $l^2\hbar^2$ (этого можно было бы ожидать) появляется комбинация $l(l+1)\hbar^2$ . Но мы еще раньше видели [например [7], в гл. 34, §7 (вып. 7)], что это обычная замена, к которой всегда приходится прибегать, если хотят, чтобы квазиклассические рассуждения совпали с правильным квантовомеханическим расчетом. Поэтому новое слагаемое можно понимать как своего рода "центробежный потенциал" положения, возникающий в уравнениях радиального движения вращающейся системы [см. [8], гл.12, §5 (вып.1)].

Теперь мы уже можем решить уравнение (2.42) относительно $F_{l}(r)$ . Оно очень похоже на (1.4), так что прибегнем к той же технике. Все повторяется вплоть до уравнения (1.15), в котором появится добавочный член

$$-l (l+1)\sum_{k=1}^{\infty}a_{k}\rho^{k-2} .$$ (2.48)

Его можно записать еще и так:

$$-l (l+1)\left\{\frac{a_{1}}{\rho}-\sum_{k=1}^{\infty}a_{k+1}\rho^{k-1}\right\}.$$ (2.49)

(Мы выделили первый член, а затем текущий индекс $k$ сдвинули на единицу.) Вместоая структура уровней энергии атома водорода (1.17) появится

$$\sum_{k=1}^{\infty}[{k(k+1)-l(l+1)}a_{k+1}-2(\alpha k-1)a_{k}]\rho^{k-1}-\frac{l(l+1)a_{1}}{\rho}=0 .$$ (2.50)

Поскольку член с $\rho^{-1}$ только один, то он должен обратиться в нуль. Коэффициент $a_{1}$ должен быть равен нулю (если только $l$ не равно нулю, но тогда мы приходим к нашему прежнему решению). А когда все квадратные скобки при любых $k$ обратятся нуль, то и все следующие члены станут равны нулю. Из - за этого условие (1.18) переходит в

$$a_{k+1}=\frac{2(\alpha k-1)}{k(k+1)-l (l+1)}a_{k}.$$ (2.51)

Это единственное существенное видоизменение по сравнению со сферически симметричным случаем.

Как и раньше, ряд должен оборваться, если мы хотим, чтобы решения представляли связанные электроны. Если $\alpha n=1$ , то ряд оборвется на $k=n$ . Условие на $\alpha$ получается таким же: $\alpha$ должно быть равно $1/n$ , где $n$ - целое число. Однако (2.51) приводит и к новому ограничению. Индекс $k$ не может быть равен $l$ , в противном случае знаменатель обратится в нуль, а $a_{l+1}$ - в бесконечность. Иначе говоря, поскольку $a_{1}=0$ , то (2.51) подразумевает, что все последовательные $a_{k}$ обращаются в нуль, пока мы не придем к $a_{l+1}$ , которое может быть и не нулем. Это означает, что $k$ должно начинаться с $l+1$ и кончаться на $n$ .

Окончательный итог таков: при любом $l$ имеется набор возможных решений, которые мы обозначим $F_{n,l}$ , где $n>l+1$ . Каждое решение соответствует состоянию

$$E_{n}=-\frac{e^4}{2\hbar^2}\left(\frac{1}{n^2}\right).$$ (2.52)

Волновая функция состояния с соответствующей функцией Гамильтона и с угловыми квантовыми числами $l$ и $m$ имеет вид

$$\psi_{n, l, m}=Y_{l, m}(\theta,\varphi)F_{n, l}(\rho),$$ (2.53)

где

$$\rho F_{n, l}(\rho)=e^{-\alpha\rho}\sum_{k=l+1}^{n}a_{k}\rho^{k} .$$ (2.54)

Коэффициенты $a_{k}$ получаются из (2.51). Наконец - то в наших руках полное описание состояний атома водорода.