2.1.  Атом водорода — как одномерная потенциальная яма

Атом водорода представляет собой систему двух взаимодействующих друг с другом частиц. Поскольку обе частицы обладают электрическим зарядом (электрон - $(-e)$ и протон - $(+e)$ ), то их взаимодействие электростатическое. Запишем одномерое уравнение Шредингера для стационарных состояний (см.[9], Э. Вихман. "Берклеевский курс физики" т. 5. Квантоваяфизика,М.,"Наука".1974г. стр. 309-316. и [10] В. А. Фок. "Начала квантовой механики" М., 2013, стр. 99-104).

$$\frac{\partial^2 \psi (T_{12})}{\partial T^2_{12}}+\frac{2}{\hbar^2}(E(T_{12})-U(T_{12}))\psi (T_{12})=0.$$ (2.55)

где расстояние $x$ определяется временем $T_{12}$ . Не зависящее от вемени $t$ это уравнение в символической форме имеет вид:

$$H\psi(T_{12})=E\psi(T_{12}).$$

Здесь $H$ -дифференциальный оператор:

$$H=-\frac{\hbar^2}{2}\frac{d^2}{dT^2_{12}}+U(T_{12}).$$

С целью сокращения и упрощения письма величину $T_{12}$ обозначим через $\tau$ , тогда уравнение (2.55) примет вид:

$$\frac{\partial^2 \psi(\tau)}{\partial\tau^2}+\frac{2}{\hbar^2}(H(\tau)-U(\tau))\psi(\tau)=0.$$ (2.56)

Введем в рассмотрение ось $x$ с началом в центре атома и направленную вдоль линии взаимодействия частиц, на которой будем откладывать числовые значения $\tau$ или равные им величины $T_{12}$ . Частица (электрон) находится в атоме в достаточно глубокой потенциальной яме, для которой $U_{1}\ll U_{2}$ . Предположим, что частица может двигаться только вдоль оси $x$ . Пусть движение ограничено практически непроницаемыми для частицы стенками: $x=0$ и $x=\tau$ . Потенциал положения $U$ имеет в этом случае следующий вид

Рис. 3.4

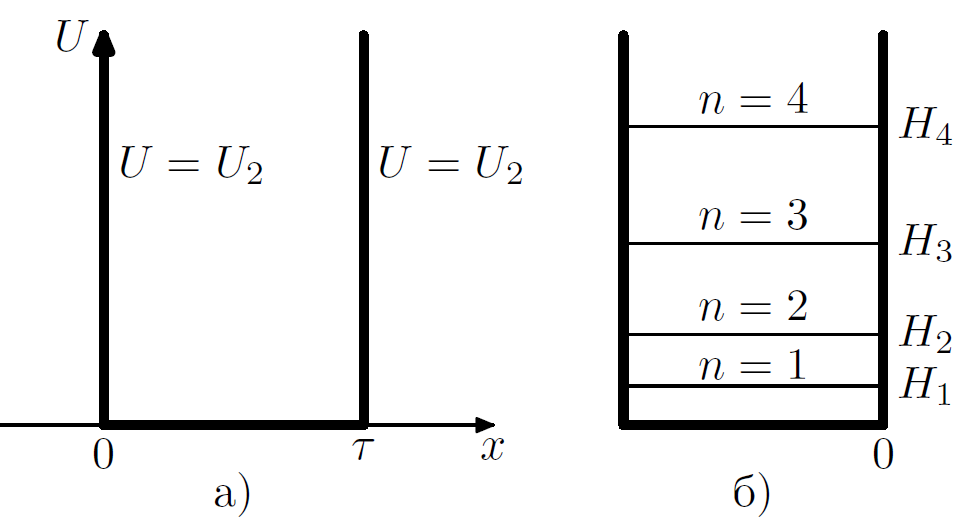
На (рис. 3.4, а) показан потенциал в точках $x=0$ и $x=\tau$ равный $U_{2}$ . За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружения частицы вне ямы равна нулю. Соответственно и функция $\psi$ за пределами ямы равна нулю. Из условия непрерывности следует, что $\psi$ должна быть равна нулю и на границах ямы, т. е. что

$$\psi (0)=\psi (\tau)=0.$$ (2.57)

Это и есть то условие, которому должны удовлетворять решения уравнения (2.56).

В области, где $\psi$ не равна тождественно нулю, уравнение (2.56) имеет вид

$$\frac{\partial^2 \psi(\tau)}{\partial\tau^2}+\frac{2}{\hbar^2}H(\tau)\psi(\tau)=0$$ (2.58)

(в этой области $U=0$ ). Введя обозначение

$$k^2=\frac{2}{\hbar^2}H,$$ (2.59)

придем к уравнению, хорошо известному из теории колебаний:

$$\psi^{\prime\prime}+k^2 \psi=0.$$

Решение этого уравнения имеет вид

$$\psi (\tau)=a\sin(k\tau+\alpha).$$ (2.60)

Условиям (2.57) можно удовлетворить соответствующим выбором постоянных $k$ и $\alpha$ . Прежде всего из условия $\psi (0)=0$ получаем

$$\psi(0)=a\sin\alpha=0,$$

откуда следует, что $\alpha$ должна быть равна нулю. Далее, должно выполняться условие

$$\psi(\tau)=a\sin k\tau=0,$$

что возможно лишь в случае, если

$$k\tau=\pm n\pi \qquad (n=1,2,3, \dots)$$ (2.61)

($n=0$ отпадает, поскольку при этом получается $\psi\equiv0$ - частица нигде не находится).

Исключив $k$ из уравнений (2.59) и (2.61), найдем собственные значения функции Гамильтона частицы:

$$H_{n}=\frac{\pi^2\hbar^2}{2\tau^2}n^2 \qquad (n=1,2,3, \dots).$$ (2.62)

Спектр функции Гамильтона оказался дискретным. На рис. 3.4, б изображена схема суммы обобщенных потенциалов скоростей и положений, т. е. уровней $H_{n}$ .

Подставив в (2.60) значение $k$ , получающееся из условия (2.61), найдем собственные функции задачи:

$$\psi_{n}(x)=a\sin(n\pi x/\tau)$$

(напомним, что $0\le x \le\tau$ и $\alpha=0$ ). Для нахождения коэффициента $a$ воспользуемся условием нормировки $\int \psi^*\psi dV=1$ , которое в данном случае запишется следующим образом:

$$a^2 \int\limits_0^\tau\sin^2\frac{n\pi x}{\tau}dx=1.$$

На концах промежутка интегрирования подынтегральная функция обращается в нуль. Поэтому значение интеграла можно получить, умножив среднее значение $\sin^2(n\pi x/\tau)$ (равное, как известно, 1/2) на длину промежутка $\tau$ . В результате получим $a^2\tau/2=1$ , откуда $a=\sqrt{2/\tau}$ . Таким образом, собственные функции имеют вид

$$\psi_{n}(x)=\sqrt{\frac{2}{\tau}}\sin\frac{n\pi x}{\tau} \qquad (n=1,2,3, \dots).$$ (2.63)

Графики собственных функций изображены на рисунке 3.5а.

Рис. 3.5

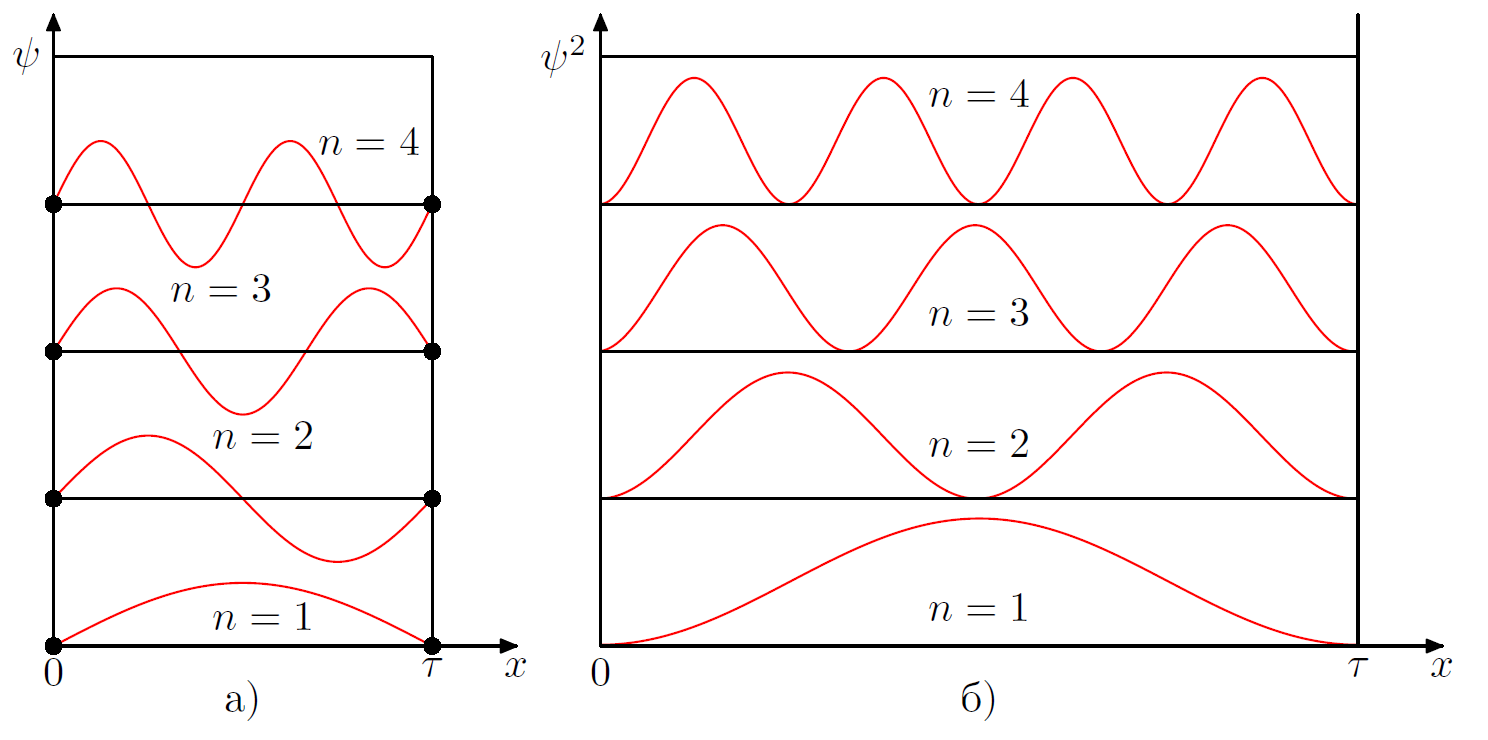
На рис. 3.5, б дана плотность вероятности обнаружения частицы на различных расстояниях от стенок ямы, равная $\psi^*\psi$ . Из графиков, например, следует, что в состоянии с $n=2$ частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Такое поведение частицы, очевидно, несовместимо с представлением о траекториях. Отметим, что согласно классическим представлениям все положения частицы в яме равновероятны.